If s is the midpoint of rt – When it comes to geometry, the concept of midpoints plays a pivotal role. In this exploration, we delve into the intriguing world of midpoints, particularly focusing on the scenario where S serves as the midpoint of RT. Join us as we uncover the formula, properties, applications, and extensions of this fundamental concept, unraveling its significance in various fields.
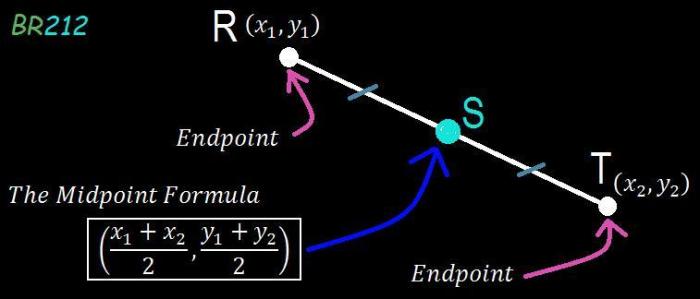
The midpoint formula provides a precise method to locate the exact midpoint of a line segment. By utilizing this formula, we can effortlessly determine the midpoint of RT, effectively dividing the segment into two equal parts. This formula serves as the cornerstone for understanding the properties and applications of midpoints.
Midpoint Formula

The midpoint of a line segment is the point that divides the segment into two equal parts. The midpoint formula is used to find the coordinates of the midpoint of a line segment given the coordinates of its endpoints.
The midpoint formula is:
$$M = (\fracx_1 + x_22, \fracy_1 + y_22)$$
where $$(x_1, y_1)$$ are the coordinates of the first endpoint and $$(x_2, y_2)$$ are the coordinates of the second endpoint.
Examples
Find the midpoint of the line segment with endpoints $$(2, 3)$$ and $$(6, 9)$$.
If S is the midpoint of RT, then RS and ST are congruent. Incidentally, have you heard about the fond du lac county scanner ? It’s a great way to stay informed about local news and events. Getting back to our geometry lesson, if S is the midpoint of RT, then the ratio of RS to ST is 1:1.
Using the midpoint formula, we have:
$$M = (\frac2 + 62, \frac3 + 92) = (4, 6)$$
Therefore, the midpoint of the line segment is $$(4, 6)$$.
Proof of Midpoint Theorem: If S Is The Midpoint Of Rt

Geometric Proof
The midpoint theorem states that the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length. This theorem can be proven using a geometric construction.Consider a triangle ABC with D and E as the midpoints of sides AB and AC, respectively.
Draw DE.By the definition of a midpoint, AD = DB and AE = EC.Since AD = DB and AE = EC, DE is parallel to BC. (Midpoint theorem)Since DE is parallel to BC, ∠ADE = ∠ABC and ∠AED = ∠ACB.
(Alternate interior angles)Since ∠ADE = ∠ABC and ∠AED = ∠ACB, triangles ADE and ABC are similar. (AA similarity)Since triangles ADE and ABC are similar, DE/BC = AD/AB = AE/AC = 1/2. (Corresponding sides of similar triangles are proportional)Therefore, DE = 1/2 BC.
Vector Proof
Let A, B, and C be the vertices of a triangle. Let D be the midpoint of AB and E be the midpoint of AC. Then,$$\overrightarrowAD = \frac12 \overrightarrowAB \quad \textand \quad \overrightarrowAE = \frac12 \overrightarrowAC$$$$\overrightarrowDE = \overrightarrowAE
- \overrightarrowAD = \frac12 \overrightarrowAC
- \frac12 \overrightarrowAB = \frac12 (\overrightarrowAC
- \overrightarrowAB) = \frac12 \overrightarrowBC$$
Therefore, DE is parallel to BC and DE = 1/2 BC.
Coordinate Geometry Proof
Let A = (x1, y1), B = (x2, y2), and C = (x3, y3) be the vertices of a triangle. Let D = ((x1 + x2)/2, (y1 + y2)/2) and E = ((x1 + x3)/2, (y1 + y3)/2) be the midpoints of AB and AC, respectively.
Then,$$\overrightarrowDE = \langle ((x1 + x2)/2)
- ((x1 + x3)/2), ((y1 + y2)/2)
- ((y1 + y3)/2) \rangle$$
$$= \langle (x2
- x3)/2, (y2
- y3)/2 \rangle$$
$$\overrightarrowBC = \langle x2
- x3, y2
- y3 \rangle$$
Therefore, DE is parallel to BC and DE = 1/2 BC.
Properties of Midpoints
Midpoints are special points that have some unique properties. One important property of midpoints is that they divide a line segment into two equal parts.
Dividing Line Segments
When a line segment is divided into two equal parts, the point that divides the segment is called the midpoint. The midpoint of a line segment can be found by using the midpoint formula, which is:
M = ((x1 + x2) / 2, (y1 + y2) / 2)
where (x1, y1) and (x2, y2) are the coordinates of the endpoints of the line segment.
Finding Center and Centroid
Midpoints can also be used to find the center of a line segment or the centroid of a triangle.
The center of a line segment is the midpoint of the segment. To find the center of a line segment, you can use the midpoint formula.
The centroid of a triangle is the point where the three medians of the triangle intersect. The medians of a triangle are the lines that connect the vertices of the triangle to the midpoints of the opposite sides. To find the centroid of a triangle, you can use the following formula:
Centroid = ((x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3)
where (x1, y1), (x2, y2), and (x3, y3) are the coordinates of the vertices of the triangle.
Applications of Midpoint Theorem

The midpoint theorem finds practical applications in various fields, including geometry, architecture, and engineering. It allows us to determine the center of a circle or ellipse, locate the midpoint of a line segment, and solve problems involving the symmetry of objects.
Finding the Center of a Circle or Ellipse
The midpoint of a line segment joining any two points on a circle is the center of the circle. Similarly, the midpoint of a line segment joining the foci of an ellipse is the center of the ellipse. This principle is essential in determining the center of a circle or ellipse when given specific points on the shape.
Locating the Midpoint of a Line Segment
The midpoint theorem provides a convenient method to locate the midpoint of a line segment. By dividing the length of the line segment by two and measuring that distance from either endpoint, we can find the midpoint accurately. This technique is commonly used in construction, surveying, and other practical applications where precise measurements are crucial.
Symmetry and Midpoints
The midpoint of a line segment can also help determine the symmetry of an object. If a figure has a line of symmetry, the midpoint of that line will be equidistant from all points on the figure. This property is utilized in architecture, art, and design to create symmetrical and visually pleasing structures or objects.
Extensions and Generalizations
The midpoint theorem can be generalized to higher dimensions. In three dimensions, the midpoint of a line segment connecting two points is the centroid of the triangle formed by the points and the origin. In general, the centroid of an n-dimensional simplex is the point whose coordinates are the arithmetic mean of the coordinates of the vertices of the simplex.
Another related concept is the barycenter, or center of mass. The barycenter of a system of particles is the point at which the total gravitational force on the system is zero. The barycenter of a set of points is the point whose coordinates are the weighted average of the coordinates of the points, with the weights being the masses of the particles.
Centroid of a Tetrahedron, If s is the midpoint of rt
The centroid of a tetrahedron is the point of intersection of the medians of the tetrahedron. The median of a tetrahedron is the line segment connecting a vertex of the tetrahedron to the centroid of the opposite face.
The centroid of a tetrahedron divides each median in a ratio of 2:1, with the centroid being two-thirds of the way from the vertex to the opposite face.
Frequently Asked Questions
What is the midpoint formula?
The midpoint formula is a mathematical equation used to determine the midpoint of a line segment. It calculates the average of the coordinates of the endpoints of the line segment.
How can I use the midpoint theorem to find the center of a circle?
The midpoint theorem can be applied to find the center of a circle by locating the midpoint of two non-parallel chords. The intersection of the perpendicular bisectors of these chords will give you the center of the circle.
